GEOMETRY in NLP

- By  Andy Coenen, Emily Reif, Ann Yuan Been Kim, 

Adam Pearce, Fernanda Viégas, Martin Wattenberg 

Google Research Cambridge, MA

Paper Link

Abstract

Transformer architectures show significant promise for natural language processing. Given that a single pretrained model can be fine-tuned to perform well on many different tasks, these networks appear to extract generally useful linguistic features. A natural question is how such networks represent this information internally. This paper describes qualitative and quantitative investigations of one particularly effective model, BERT. At a high level, linguistic features seem to be represented in separate semantic and syntactic subspaces. We find evidence of a fine-grained geometric representation of word senses. We also present empirical descriptions of syntactic representations in both attention matrices and individual word embeddings, as well as a mathematical argument to explain the geometry of these representations.

Language is made of discrete structures, yet neural networks operate on continuous data: vectors in high-dimensional space. A successful language-processing network must translate this symbolic information into some kind of geometric representation—but in what form? Word embeddings provide two well-known examples: distance encodes semantic similarity, while certain directions correspond to polarities (e.g. male vs. female).

A recent, fascinating discovery points to an entirely new type of representation. One of the key pieces of linguistic information about a sentence is its syntactic structure. This structure can be represented as a tree whose nodes correspond to words of the sentence. Hewitt and Manning, in A structural probe for finding syntax in word representations, show that several language-processing networks construct geometric copies of such syntax trees. Words are given locations in a high-dimensional space, and Euclidean distance between these locations maps to tree distance.

But an intriguing puzzle accompanies this discovery. The mapping between tree distance and Euclidean distance isn't linear. Instead, Hewitt and Manning found that tree distance corresponds to the square of Euclidean distance. They ask why squaring distance is necessary, and whether there are other possible mappings.

This note provides some potential answers to the puzzle. We show that from a mathematical point of view, squared-distance mappings of trees are particularly natural. Even certain randomized tree embeddings will obey an approximate squared-distance law. Moreover, just knowing the squared-distance relationship allows us to give a simple, explicit description of the overall shape of a tree embedding.

Tree embeddings in theory

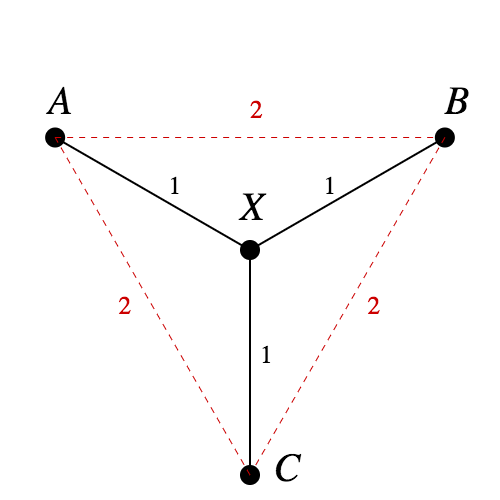
If you're going to embed a tree into Euclidean space, why not just have tree distance correspond directly to Euclidean distance? One reason is that if the tree has branches, it's impossible to do isometrically.

In fact, the tree in Figure 1 is one of the standard examples to show that not all metric spaces can be embedded in RnRn isometrically. Since d(A,B)=d(A,X)+d(X,B)d(A,B)=d(A,X)+d(X,B), in any embedding AA, XX, and BB will be collinear. The same logic says AA, XX, and CC will be collinear. But that means B=CB=C, a contradiction.

If a tree has any branches at all, it contains a copy of this configuration, and can't be embedded isometrically either.

Pythagorean embeddings

By contrast, squared-distance embeddings turn out to be much nicer—so nice that we'll give them a name. The reasons behind the name will soon become clear.

Definition: Pythagorean embedding

Let MM be a metric space, with metric dd. We say f:M→Rnf:M→Rn is a Pythagorean embedding if for all x,y∈Mx,y∈M, we have d(x,y)=∥f(x)−f(y)∥2d(x,y)=‖f(x)−f(y)‖2.

Does the tree in Figure 1 have a Pythagorean embedding? Yes: as seen in Figure 2, we can assign points to neighbouring vertices of a unit cube, and the Pythagorean theorem gives us what we want.

What about other small trees, like a chain of four vertices? That too has a tidy Pythagorean embedding into the vertices of a cube.

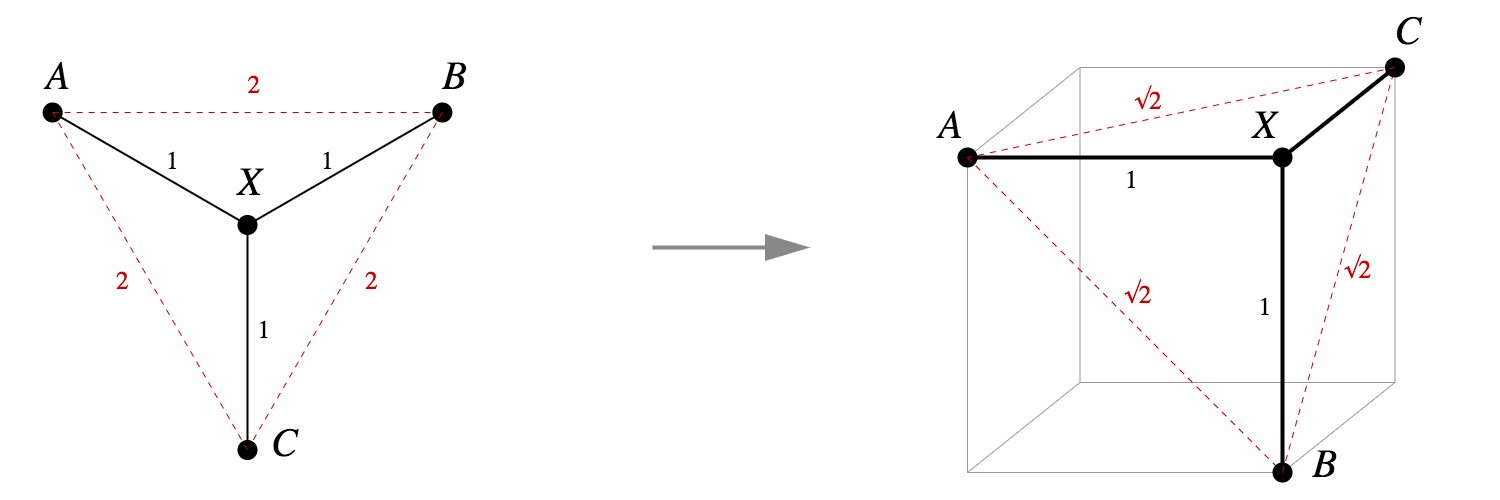
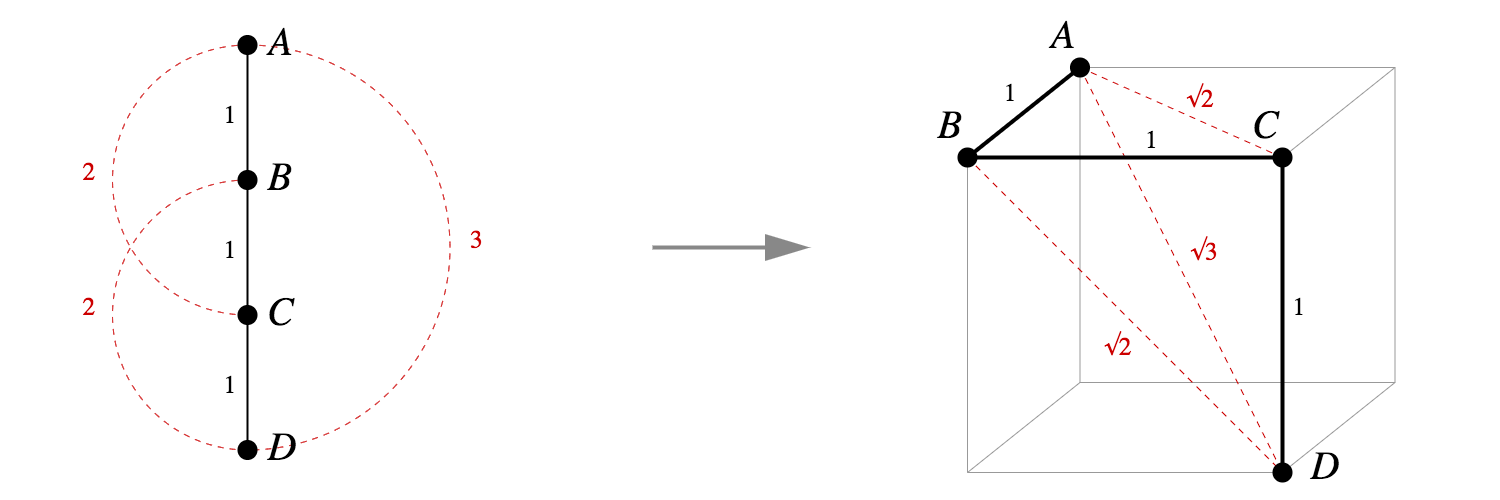
It's actually straightforward to write down an explicit Pythagorean embedding for any tree into vertices of a unit hypercube.

Visualization of Trees

Conclusion

Exactly how neural nets represent linguistic information remains mysterious. But we're starting to see enticing clues. The recent work by Hewitt and Manning provides evidence of direct, geometric representations of parse trees. They found an intriguing squared-distance effect, which we argue reflects a mathematically natural type of embedding—and which gives us a surprisingly complete idea of the embedding geometry. At the same time, empirical study of parse tree embeddings in BERT shows that there may be more to the story, with additional quantitative aspects to parse tree representations.